TIPOLOGÍA DE PARTIDOS Y FACTORES DE RENDIMIENTO EN BALONCESTO

Martínez, J.A.¹ yMartínez, L.²

¹Profesor Contratado Doctor. Departamento de Economía de la Empresa. Universidad Politécnica de Cartagena. España. http://www.upct.es/~beside/jose, josean.martinez@upct.es

²Profesora Contratada Doctora. Departamento de Economía de la Empresa. Universidad Politécnica de Cartagena. España. http://www.upct.es/~beside/laura, laura.martinez@upct.es

Martínez, J.A. y Martínez, L.(2013). Tipología de partidos y factores de rendimiento en baloncesto / Typology of games and performance factors in basketball. Revista Internacional de Medicina y Ciencias de la Actividad Física y el Deporte vol. 13 (49) pp.131-148.

Código UNESCO / UNESCO Code: 5899 Educación Física y Deporte / Physical Education and Sport

Clasificación Consejo de Europa / Europe Council classification: 17 Otras (Análisis cuantitativo del deporte) / OTHER (Quantitative analysis of sport)

Recibido 25 de enero de 2011 Received January 25, 2011

Aceptado 15 de junio de 2011 Accepted June 15, 2011

RESUMEN

Esta investigación analiza la tipología de partidos de baloncesto utilizando una aproximación probabilística para la solución cluster, e incorporando factores de rendimiento, así como variables exógenas que influyen en la probabilidad de victoria, y por ende, en la diferencia final en el marcador. Tras analizar datos de partidos de la NBA, implementar varios procesos de filtrado, y realizar dos replicaciones añadidas, los resultados muestran que existen cinco tipologías de partidos diferentes, tomando como referencia principal la diferencia en el marcador. Así, las variables más importantes para discriminar entre los diferentes clusters son el margen de puntos, la eficiencia en el lanzamiento y la diferencia de potencial entre los contendientes. Consideraciones sobre el factor cancha, los factores de rendimiento, los métodos de análisis y la endogeneidad de las variables son discutidas.

PALABRAS CLAVES: Baloncesto, rendimiento, análisis cluster, tipología de partidos.

ABSTRACT

This research uses a probabilistic clustering technique to establish a typology of basketball games, considering several performance factors and exogenous variables influencing the probability of winning a game. After analysing NBA data, implementing several filtering processes, and achieving two successive replications, results show that there are five different types of games. The most important variables to discriminate among clusters are the margin of points, the effective field goal percentage and the winning percentage difference between teams. Considerations regarding the home/field advantage, the performance factors, the method to analyse data, and the endogeneity of variables are discussed.

KEYWORDS: Basketball, performance, cluster analysis, game profiles.

1. INTRODUCCIÓN

Una de las líneas de trabajo desarrolladas en los últimos años en el análisis del rendimiento de equipos de baloncesto es la identificación de tipologías de partidos (ver Gómez, Lorenzo y Sampaio, 2009). Así, se suele distinguir los partidos en función de su equilibrio en el marcador (normalmente en tres o cuatro niveles de equilibrio), y se analizan los factores asociados a la victoria en cada uno de esos grupos de partidos. La importancia de este análisis radica en el hecho de que esas variables relacionadas con la victoria son distintas en función del tipo de partido, por lo que las conclusiones sobre los elementos relacionados con el éxito difieren para cada cluster. Esos clusters representan las diferentes tipologías de partidos, donde cada cluster tiene unas características homogéneas que, a su vez, lo distingue de los demás.

Gómez, Lorenzo y Sampaio (2009) revisan numerosas investigaciones que han tratado este tema, en un recorrido por diferentes competiciones, y cuyos resultados, en la mayoría de los casos, son fruto de análisis estadístico de segmentación (K-means), o de una simple división en base a criterios subjetivos. Sin embargo, y a pesar de esa meritoria revisión, los resultados descritos muestran carencias conceptuales y metodológicas que podrían minimizarse (al menos en gran parte) con la adopción de una perspectiva de investigación diferente. Así, se necesitan discutir cuatro elementos fundamentales que no son tratados con suficiencia en las investigaciones revisadas, ni tampoco en los estudios empíricos de estos autores: (1) el papel de la ventaja campo; (2) la existencia de los “4 factores” de rendimiento; (3) la elección del método de segmentación; (4) la posible endogeneidad de las variables utilizadas.

En cuanto al factor campo, y circunscrito a la NBA, Winston (2009) muestra cómo existe un diferencial de 3.2 puntos favorable al equipo de casa. Esto indica que no se deben establecer tipologías de partidos sin considerar ese margen. O dicho de otro modo, no es lo mismo derivar conclusiones de un partido cuya diferencia final en el marcador es, por ejemplo, de 8 puntos si ese partido lo ha ganado el equipo local o el visitante. Así, si ha ganado el equipo visitante, éste ha tenido que superar no sólo al equipo rival, sino al margen asociado al factor campo. Por tanto, los partidos no debieran dividirse de la forma “partidos cuya diferencia es de 1 a 8 puntos”, sino “partidos en casa cuya diferencia a favor es de XXX puntos”, y “partidos en casa cuya diferencia en contra es de XXX puntos”.

Otro elemento esencial está relacionado con una de las aportaciones más relevantes realizadas por Oliver (2004) al ámbito del análisis del baloncesto, y es la identificación de cuatro factores de desempeño que explican de forma casi perfecta los resultados de los partidos. Esos cuatro factores se calculan para cada equipo, y se refieren a la efectividad en el lanzamiento, los balones perdidos por posesión, el porcentaje de rebotes ofensivos sobre los lanzamientos fallados, y los tiros libres convertidos sobre los lanzamientos de campo intentados. Esas cuatro variables, que pueden derivarse fácilmente del box-score de cada partido, explican más del 90% de la variación en el número de victorias de los equipos (Winston, 2009). Por tanto, ya existe una muy certera identificación de factores asociados a la victoria de los equipos, que cuenta con la ventaja añadida de su baja correlación, lo que los hace muy atractivos para su interpretación estadística. De este modo, no se tienen los inconvenientes de la multicolinealidad que surge de analizar las estadísticas básicas del box-score, tal y como, por ejemplo, Gómez, Lorenzo y Sampaio (2009) realizan. Hay que tener en cuenta que en la NBA, la correlación entre lanzamientos intentados y fallados es alrededor de 0,5, lo que significa que son variables altamente asociadas, y que su inclusión conjunta en modelos lineales, como la regresión o el análisis discriminante, puede ocasionar problemas derivados de la multicolinealidad.

En relación al método de segmentación utilizado, se tiende a implementar un análisis de conglomerados denominado K-means. Aunque este análisis puede proporcionar resultados válidos, no es menos cierto que ha sido criticado por la arbitrariedad en la determinación del número de clusters, al margen de por otras limitaciones en su aplicación. Así, Magidson y Vermunt (2002) recomiendan el uso de una extensión probabilística de este método, denominado análisis de clases latentes, y que cubre muchas de las limitaciones del algoritmo K-means, siendo la principal ventaja la determinación estadística del número de clusters, además de la posibilidad de inclusión de variables medidas en diferentes tipos de escala, o la consideración de variables exógenas como covariables en la misma estimación. Como muestran Vermunt y Magidson (2005), este análisis puede ser implementado a través de un software comercial y de fácil manejo, como Latent Gold. Aunque existen multitud de métodos de segmentación, ciertamente no hay ningún procedimiento perfecto. Como indican Xu y Wunsch II (2009) siempre hay ciertas dosis de subjetividad en el proceso de agrupación, independientemente del método utilizado. No obstante, y reconociendo la naturaleza exploratoria de ese proceso inductivo, las técnicas mencionadas pueden proporcionar unos resultados más consistentes desde el punto de vista metodológico.

Finalmente, no existe discusión alguna sobre la posible endogeneidad de las variables utilizadas en el análisis. Recordemos que una variable es endógena cuando, al funcionar como predictor en el ámbito del modelo lineal general de probabilidad, el término de error del modelo está correlacionado con esa variable, por lo que se rompen los supuestos básicos de ciertas estimaciones, como las de la clásica estimación por mínimos cuadrados de la regresión lineal (ver Wooldridge, 2003). Esto ocurre, por ejemplo, cuando existen relaciones recíprocas entre las variables, fruto en ocasiones de la ocurrencia de un proceso dinámico (Kline, 2010). Este hecho ha sido tratado recientemente por Arkes (2011), en el análisis de la importancia de las estadísticas de juego sobre la victoria de los equipos en la Liga Americana de Football. Arkes (2011) admite que las estadísticas de juego son parcialmente influenciadas por el propio resultado del partido en cada momento, por lo que tienen un carácter endógeno. Así, no son factores exógenos manipulables o de intervención, sino que parcialmente son fruto de la propia dinámica del juego y resultados. Arkes (2011) adopta una perspectiva conservadora al respecto, considerando sólo las estadísticas de la primera parte de los partidos.

Si las variables derivadas del box-score son endógenas, entonces la interpretación sobre la influencia de esas variables en el resultado final está sesgada. Por tanto, quedaría algo desvirtuada cualquier inferencia causal. Bien es cierto que tanto Gómez, Lorenzo y Sampaio (2009), como Winston (2009), o incluso Berri (2008) cuidan mucho el lenguaje y hablan de “asociación” más que de “determinación” o “influencia”, lo que es en verdad prudente. Sólo Arkes (2011) habla firmemente de exogeneidad en el uso de las variables de la primera parte de los partidos para “causar” el éxito en el resultado final. Aunque el razonamiento de Arkes (2011) puede ser criticado por su propia circularidad (un partido es un sistema dinámico desde que comienza, y no sólo desde la mitad del mismo), su propuesta se acerca más a lo que debiera ser un modelo que proporcione información sobre efectos causales.

Una posible solución sería la utilización de variables instrumentales y el test de Hausman (ver Wooldridge, 2003). Sin embargo, encontrar al menos 4 variables instrumentales adecuadas para el modelo de los 4 factores resulta complejo. Aunque las variables utilizadas por Martínez (2011a) en su modelo son completamente exógenas (se refieren al día de descanso entre partidos, rachas de equipos, diferencia de potencial y calidad del partido), los efectos de algunas de ellas son mínimos, por lo que su correlación con las variables endógenas podría no existir y, de este modo, no ser válidas como instrumento de estimación. Además, aunque las variables del modelo de Martínez (2011a) son exógenas y explican con un adecuado nivel de acierto la probabilidad de victoria, no son variables susceptibles de ser manipuladas, algo inherente a la utilidad de los modelos causales (ver Pearl, 2000). Por tanto, explican y predicen la victoria, pero los equipos poco pueden hacer para influir en ellas.

En cualquier caso, la existencia de esa endogeneidad, aunque teóricamente poco cuestionable, no debiera producir efectos prácticos importantes. Aunque esto es sólo una conjetura (difícil de contrastar por el problema de los instrumentos comentado anteriormente), creemos que tiene una base sólida. Sin embargo, consideramos prudente no tomar como variables independientes o covariables aquellas que puedan ser susceptibles de ser endógenas, como los factores de rendimiento de cada partido, pero sí aquellos factores que caracterizan cada partido antes de que éste suceda, como los analizados por Martínez (2011a). Por otro lado, la utilización de un procedimiento robusto de recorte de los datos para eliminar valores extremos (ver Wilcox, 2010) sería altamente recomendable, ya que así se eliminarían los partidos con diferencias extremas en el resultado, los cuales son, precisamente, las partidos donde el fenómeno de endogeneidad es posible que aparezca con más fuerza.

Este trabajo contribuye de forma novedosa a la investigación sobre detección de perfiles de partidos y factores de rendimiento desde la óptica explicada anteriormente, y analiza empíricamente un volumen de datos mayor que las investigaciones revisadas en Gómez, Lorenzo y Sampaio (2009), incluyendo además dos replicaciones sucesivas, lo que confiere gran robustez. Por tanto, el objetivo es establecer una tipología de partidos de baloncesto en función de las variables de rendimiento (4 factores) y de las variables exógenas que influyen en el resultado final. Para ello, aplicaremos un tratamiento estadístico conservador, realizando un análisis de segmentación de clases latentes tomando como indicadores el margen de puntos y los cuatro factores de Oliver (2004), y como covariables las variables exógenas propuestas por Martínez (2011a). Además, consideraremos las diferencias parciales en el marcado en los cuartos de los partidos, lo que ayudará a caracterizad los clusters. Tras la eliminación de valores extremos de los datos, realizaremos un análisis de la temporada 2006/07 en la NBA, implementando una doble replicación de los resultados para las dos temporadas subsiguientes.

2. MÉTODOLOGÍA

Se utilizó una base de datos compactada de las temporadas 2006/07, 2007/08 y 2008/09 (en su fase regular), adquirida en www.nbastuffer.com, con los resultados de todos los partidos y sus estadísticas básicas. Por tanto, el archivo reflejaba un total de 3690 partidos (1230 por temporada).

 A través de las estadísticas del box-score descritas en la base de datos, se calcularon los 4 factores y su diferencial entre equipos. Se tomó como referencia el equipo que jugaba en casa, por lo que todas las variables están relativizadas al equipo titular de la cancha de juego. Así, el margen de puntos de cada partido tiene un signo negativo si el equipo de casa resultó perdedor. Además, se computaron la diferencia acumulada en el primer, segundo y tercer cuarto de cada partido, con el fin de tener más información que ayudara a perfilar los clusters.

Como variables exógenas se consideraron las explicadas por Martínez (2011a): diferencia entre días de descanso, diferencia entre el número de victorias en los últimos 5 partidos (factor de rachas de juego), diferencia entre el porcentaje de victorias en el momento del partido, y el factor de calidad del partido. Esta última variable necesita una mayor explicación, ya que su entendimiento es menos intuitivo y evidente. Representa el valor absoluto de la diferencia entre el porcentaje de victorias de los equipos transformado en función de un parámetro exponencial 1/λ. En la NBA existe interacción entre la ventaja campo y la calidad de los equipos. Los equipos con menor potencial son relativamente más fuertes en casa que aquellos con mayor potencial. Por tanto, el valor del parámetro hace referencia a la suma del potencial de ambos equipos (mínimo cero y máximo dos). De este modo, para equipos con una diferencia de potencial similar, el valor del factor de calidad del partido se incrementa si los dos equipos tienen un porcentaje de victorias elevado en comparación a si lo tienen bajo. Por ejemplo, esta variable es 0,63 cuando se enfrentan dos equipos con porcentaje de victorias 1 y 0,5, respectivamente. Mientras que su valor es de 0,31 si ambos equipos tienen porcentajes de 0,6 y 0,1 respectivamente. Es decir, ante la misma diferencia de potencial, el factor de calidad del partido corrige por el potencial de ambos equipos Es una variable acotada en un rango [0,1]

Una vez identificadas las variables del análisis, se procedió a realizar una depuración de los datos. En primer lugar, se siguieron las recomendaciones de Wilcox (2010) para recortar un 5% de ambas colas de la distribución de datos ordenados (obviamente se escogió el margen de puntos como variable objetivo). Esto se implementó independientemente para cada una de las temporadas. Así, la distribución está libre de valores extremos que podrían distorsionar cualquier análisis posterior, resultando la pérdida de información poco relevante, ya que sólo se eliminaron 372 casos de los 3690 totales (369 más 3 casos añadidos por la división decimal).

Después, y siguiendo las recomendaciones de Martínez (2011b), se eliminaron los primeros partidos de la temporada para cada equipo. Concretamente, sólo se consideraron aquellos partidos en los que ambos equipos habían jugado ya al menos 19 partidos anteriores. El motivo de ese recorte es incrementar la fiabilidad de la variable referida a la diferencia entre el porcentaje de victorias de ambos equipos en el momento del partido. En los primeros partidos de la temporada, el porcentaje de victorias actual no es un buen estimador del porcentaje de victorias final, ya que existe un error importante. A medida que la temporada avanza, la aproximación se hace mejor, y a partir de los 10 primeros partidos el error va disminuyendo de manera más acuciante. Como disponemos de un gran volumen de datos, hemos optado por realizar un recorte mayor (19 primeros partidos), donde los niveles de error son ciertamente más bajos. Otra opción hubiera sido el no hacer ningún recorte de este tipo y tomar el porcentaje de victorias final como variable Proxy de la calidad de los equipos, o incluso realizar 2 o 3 particiones de la temporada y tomar esa variable para cada partición. Sin embargo, esa información es una información que no se conoce a priori, es decir, antes de cada partido, por lo que si se quiere realizar una predicción, no sería adecuado utilizarlas. Por tanto, en nuestro caso, nos hemos enfocado más en la predicción que la explicación, con el fin de que los resultados obtenidos puedan ser utilizados para realizar predicciones a partir de la situación de los equipos antes de cada partido. Un proceso parecido de filtrado se ha utilizado en modelos predictivos en la NBA, como el que se muestra en www.nbastuffer.com

Finalmente, y tras estos procesos de depuración de datos, un total de 2526 partidos fueron sometidos a un análisis de segmentación de clases latentes (840, 845 y 841 por temporada), utilizando el programa Latent Gold (Vermunt y Magidson, 2005).

3. RESULTADOS

Se especificó un análisis cluster en Latent Gold, en cuya terminología (ver Vermunt y Magidson, 2005) los indicadores eran los 4 factores de rendimiento y el margen de puntos, y las covariables la diferencia acumulada en los tres primeros cuartos de cada partido y las variables “pre-partido” comentadas anteriormente. Éstas últimas fueron etiquetadas como covariables activas, dada su exogeneidad, y las primeras como inactivas, por su dependencia con los indicadores.

Se aplicó el análisis para cada una de las temporadas, obteniendo una mejor solución estadística de 5 clusters para cada una de ellas, atendiendo al criterio de menor BIC (Tabla 1). Sólo para la temporada 2007/08 la solución de 6 clusters es similar, aunque en realidad, el cambio en BIC es prácticamente irrelevante. Recordemos que el BIC hace referencia al Criterio de Información Bayesiano calculado a partir del logaritmo de verosimilitud, el tamaño de la muestra y los grados de libertad (Vermunt y Magidson, 2005). Es un criterio de elección de modelos donde prima el valor más bajo, y básicamente se refiere a un índice de ajuste del modelo a los datos observados teniendo en cuenta la complejidad del modelo (parsimonia) y el tamaño de la muestra.

Tabla 1. Estadísticos de los modelos

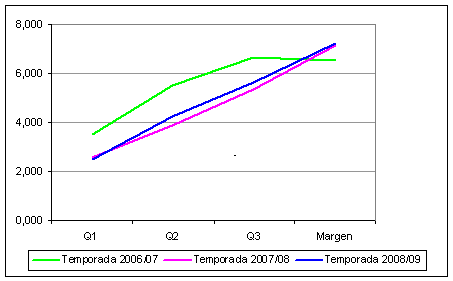
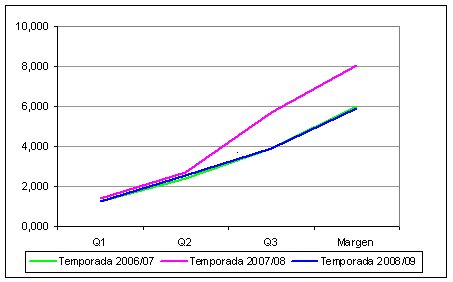
Una muestra de la homogeneidad de la solución cluster encontrada para cada temporada se refleja gráficamente en las Figuras 1 y 2, donde se representan las medias de cada variable en los cinco clusters identificados.

Como puede apreciarse en la Figura 1, el tamaño de los clusters es prácticamente idéntico en cada temporada, así como las medias de los 4 factores, la diferencia en el porcentaje de victorias y el factor de calidad de cada partido. Sólo la diferencia en rachas y días de descanso es un poco divergente, pero hay que tener en cuenta que el rango de esas variables es mucho menor (entre los 10 y los 12 valores). No obstante, esas divergencias no van más allá de unas dos décimas.

La Figura 2 muestra un nivel de homogeneidad también muy alto entre el promedio de margen de puntos, y las diferencias acumuladas para cada cuarto (Q1, Q2 y Q3).

Figura 1. Homogeneidad de la solución cluster para cada uno de los 5 tipos de partidos (I)

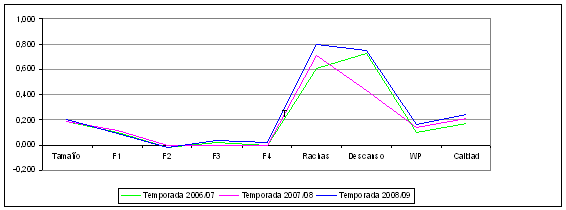
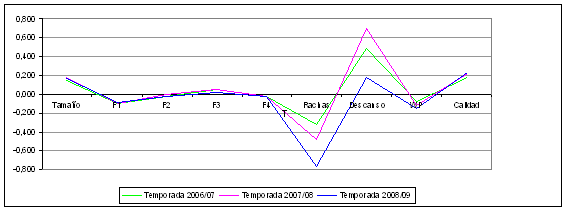
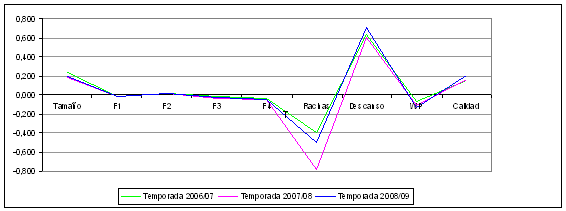
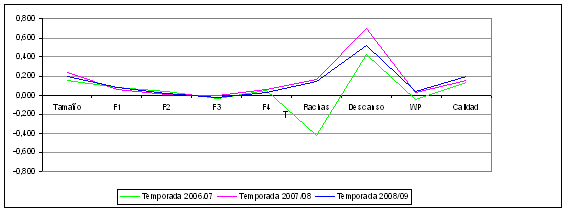
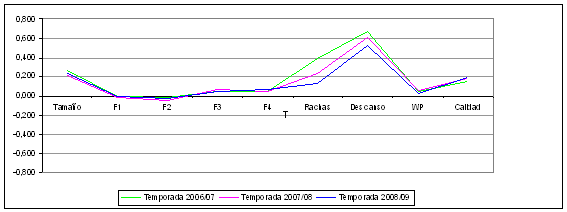
Figura 2. Homogeneidad de la solución cluster para cada uno de los 5 tipos de partidos (II)

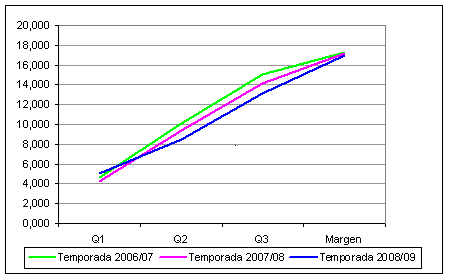
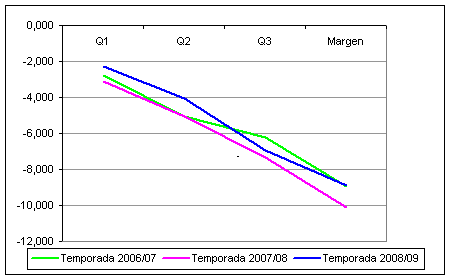
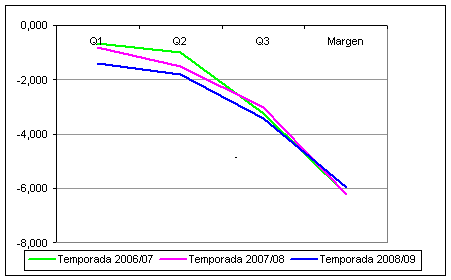
Aunque la homogeneidad en cuanto a promedios parece evidente, sería también de interés estudiarla respecto a distribuciones. Recordemos que dos variables pueden tener una media similar pero ser totalmente opuestas en su distribución, lo que iría en contra de la homogeneidad que queremos constatar.

Para ello, realizamos todas las comparaciones posibles 2 a 2 entre las 9 variables activas (no se incluyen las covariables inactivas), las 3 temporadas y los 5 clusters (utilizando la asignación modal de Latent Gold). En total 135 comparaciones que se testaron a través de la prueba no paramétrica de Wilcoxon-Mann-Whitney. Un 40% de parejas de comparaciones resultaron no significativas, o lo que es lo mismo, no se puede rechazar la hipótesis de igualdad de distribución. Éste es un porcentaje bastante alto dado el carácter exploratorio de la solución cluster, e indica que no sólo las medias son similares entre clusters, sino que una parte importante de los datos se distribuyen de la misma forma.

Por tanto, y dado que la uniformidad en los segmentos encontrados es alta, tenemos un respaldo suficiente para pasar a interpretar los diferentes clusters. Realizaremos los comentarios para la temporada 2006/07, ya que para las dos replicaciones sucesivas la solución cluster ofrece resultados similares. La caracterización de los diferentes clusters debe hacerse visionando conjuntamente las Figuras 3, 4 y 5. No obstante, es preceptivo indicar, que todas las variables son significativas para discriminar entre clusters salvo 3 de las 4 exógenas (diferencia en rachas, diferencia en descanso y calidad del partido). De este modo, sólo la diferencia en porcentaje de victorias tiene un efecto significativo en la solución cluster. Además, desde el punto de vista de varianza explicada, tanto el margen de puntos, como la eficiencia en el lanzamiento tendrían valores por encima del 80 y el 70%, respectivamente, mientras que los balones perdidos obtendrían alrededor de la tercera parte. Así, los últimos 2 factores (rebotes ofensivos sobre lanzamientos fallados y tiros libres sobre tiros de campo) tendrían una contribución marginal a la varianza (sobre el 7%). Por tanto, y a la hora de comentar los clusters, hay que tener en cuenta de que las variables más relevantes son el margen de puntos, la eficiencia en el lanzamiento y la diferencia de potencial entre equipos, y en menor medida los balones perdidos por posesión.

Figura 3. Diferencia en el marcador

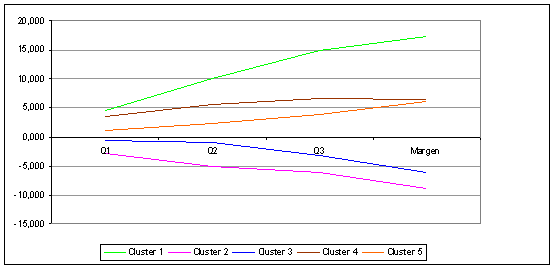
Figura 4. Cuatro factores de rendimiento

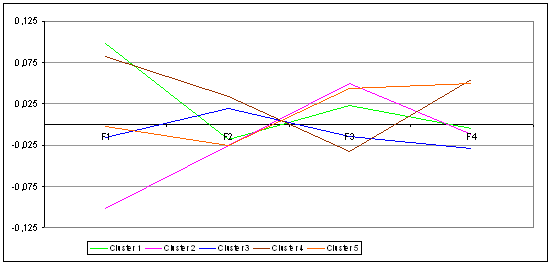
Figura 5. Variables exógenas

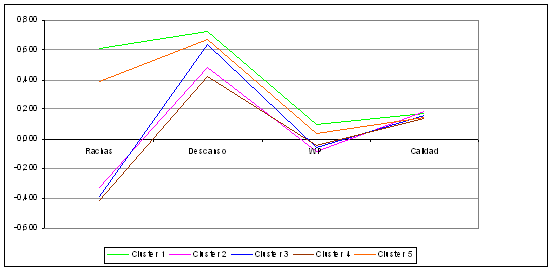
Así, un primer tipo de partidos estaría definido por grandes diferencias en el marcador para el equipo de casa (con un promedio superior a los 15 puntos). En esos partidos, el equipo local dominaría el marcador desde el primer cuarto, aumentando su ventaja considerablemente a medida que el partido avanza. La diferencia en la eficiencia en el lanzamiento del equipo local en relación al visitante sería bastante acusada (alrededor de una décima), lo que sería indicativo de un nivel de acierto relativo muy superior. Además, el equipo ganador pierde menos balones por posesión y consigue un mayor porcentaje de rebotes ofensivos sobre tiros fallados. Es decir, no sólo lanza ostensiblemente con más acierto, sino que rebotea porcentualmente mejor los lanzamientos que falla. En cuanto a las variables exógenas, en este tipo de partidos el equipo local viene de una mejor racha de resultados que el visitante y dispone de más días de descanso, además de que la diferencia en el porcentaje de victorias es la más elevada de todas (por encima de 0,1 unidades en promedio).

Un segundo tipo de partidos tendría un comportamiento opuesto al primero. Aquí los equipos visitantes ganarían por una diferencia de unos 9 puntos en promedio, consiguiendo también dominar todo el partido, aunque de manera menos clara que el primer cluster. En cuanto a los cuatro factores, la eficiencia en el lanzamiento y los balones perdidos se comportarían de manera también opuesta al primer cluster, con la diferencia de que el porcentaje de rebotes ofensivos sobre tiros fallados sería favorable al equipo local. Este hecho, muy posiblemente hace que no se consiga un margen final de puntos similar al del cluster 1, ya que aunque el equipo visitante lanza mejor y pierde menos balones, no consigue relativamente tan buen desempeño reboteador, lo que da otras opciones al equipo local para lanzar. Serían partidos en los que el equipo local tendría un potencial de unos 0,08 unidades en promedio peor que el visitante.

El tercer tipo de partidos es similar al segundo tipo en el sentido que el equipo visitante también consigue la victoria, aunque por un margen menor. Son partidos mucho más igualados, que se decantan al final por una diferencia más ajustada. Esa igualdad también queda reflejada en los 4 factores de rendimiento, donde para los dos primeros se cumple el mismo patrón anterior (el equipo que gana es más eficiente en el lanzamiento y pierde menos balones). En este caso, la diferencia de potencial es menor (del orden de 0.06 unidades en promedio). Es decir, son partidos más igualados porque el potencial de los equipos es más parejo y su rendimiento en el campo también.

Finalmente, comentaremos conjuntamente los clusters 4 y 5, ya que tienen algunas particularidades. Así, ambos tipos de partidos se resuelven para el equipo local con una diferencia similar en el marcador (sobre los 6 puntos de media), aunque en el cluster 5 el partido es en general más igualado. Sin embargo, el comportamiento de los 4 factores de rendimiento es mucho menos claro que en los clusters anteriores. Así, el cluster 4 se caracteriza porque el equipo local lanza mucho mejor que el visitante, aunque pierde relativamente más balones. Esa efectividad en el lanzamiento hace que, aunque el equipo local tenga un potencial más bajo (la diferencia en el porcentaje de victorias es negativa), pueda finalmente ganar el partido. Sin embargo, los partidos del cluster 5 se caracterizan porque el equipo local, que es el ganador, se desempeña peor en los 2 factores principales (eficiencia en el lanzamiento y balones perdidos) que el visitante, aunque es mejor en el rebote ofensivo y en los tiros libres. Este último factor, los lanzamientos libres convertidos sobre tiros de campo intentados es quizá lo que más diferencia a los clusters 4 y 5 del resto, y que puede ser una de las claves para interpretar su comportamiento. Así, hay que tener en cuenta que en las tres temporadas de análisis los equipos locales que ganaron el partido fueron castigados con casi 2 personales menos que los visitantes, mientras que para los que perdieron el diferencial es de 0,65 a favor del equipo de casa. Esto indica que en las victorias locales los árbitros pitan generalmente más faltas personales al equipo visitante, lo que se traduce en una mayor oportunidad de conseguir anotar desde el tiro libre para el equipo local, a la postre ganador del partido.

4. DISCUSIÓN

Esta investigación ha adoptado una perspectiva novedosa para el análisis de tipología de partidos de baloncesto, utilizando una aproximación probabilística para la solución cluster, e incorporando los 4 factores de rendimiento propuestos por Oliver (2004), así como variables exógenas que influyen en la probabilidad de victoria, y por ende, en la diferencia final en el marcador.

Tras analizar un elevado volumen de datos, implementar varios procesos de filtrado, y realizar dos replicaciones añadidas, los resultados muestran que existen 5 tipologías de partidos diferentes, tomando como referencia principal la diferencia en el marcador.

La diferencia de potencial en el momento del partido entre los dos equipos es la única variable exógena que discrimina de manera relevante entre clusters. Así, para los clusters 1, 2 y 3, donde las diferencias en el marcador son en promedio más elevadas, es donde se observan mayores niveles de diferencia en esa variable. Por tanto, a la hora de realizar predicciones sobre cuál será el margen de puntos final de un partido, la diferencia de potencial entre los equipos es un factor a tener en cuenta. A medida que la diferencia aumenta para el equipo local, será más probable que los partidos acaben una diferencia mayor positiva, mientras que ocurriría lo contrario si es el equipo visitante quien está mejor posicionado en la tabla clasificatoria.

Los partidos correspondientes a esos 3 clusters se caracterizan por un patrón similar en la eficiencia en el lanzamiento y en los balones perdidos. Así, a medida que el margen se incrementa, varían de forma similar esos factores de rendimiento, que por otro lado, son los más importantes. De este modo, tanto el porcentaje de rebotes ofensivos sobre lanzamientos fallados, como el porcentaje de tiros libres sobre lanzamientos intentados contribuyen de forma mucho menor a la discriminación entre clusters. Sin embargo, este último factor tiene más relevancia para explicar la diferencia entre los clusters 4 y 5 y los demás. Así, para los partidos más igualados que se resuelven finalmente para el equipo local, las faltas personales se convierten en un elemento importante, ya que los equipos locales tienen un diferencial mayor en este factor con respecto a sus rivales (les pitan más faltas a los equipos visitantes, por lo que los equipos locales van más a la línea de personal).

Este último hecho puede ser una de los efectos que la “ventaja campo” confiere a los equipos, donde la presión ambiental podría condicionar de alguna manera a los árbitros, o simplemente, que el equipo local es más incisivo y provoca más faltas a sus rivales. En cualquier caso, esto no es más que una muestra de cómo el factor cancha influye en el resultado final de un partido, y cómo hay que tenerlo en cuenta para cualquier análisis que pretenda caracterizar partidos. Además, los equipos locales descansan como media 0,6 unidades más que los visitantes, por lo que cuentan con la ventaja teórica añadida de más tiempo de recuperación entre partidos.

No obstante, y como muy bien muestran Gómez, Lorenzo y Sampaio (2009), existen otras competiciones que se juegan en terreno neutral, como los diferentes campeonatos de selecciones, donde sería interesante que futuros estudios profundizaran en la caracterización de partidos. Así, no existiría ventaja campo (sólo para el equipo anfitrión), aunque tal vez habría que moderar por factores relativos al apoyo del público.

Por tanto, a la hora de realizar predicciones, sobre todo si se es apostante, sería mucho más seguro considerar sólo aquellos partidos en los que la diferencia de potencial a priori entre los equipos fuera más grande. Aunque esto pueda parecer una obviedad, empíricamente hemos mostrado que cuando el diferencial es mayor en promedio de 0,06 para el equipo visitante, la probabilidad de que este gane el partido por más de 5 puntos es alta, mientras que si esa diferencia está en torno a 0,1 para el equipo local, lo más probable que es que consiga ganar el partido de forma muy amplia. Sin embargo, cuando la diferencia de potencial es menos clara entre los equipos, sería mucho más arriesgado predecir el margen final de puntos, ya que como muestran los clusters 4 y 5, el partido puede resolverse para el equipo de casa por un margen similar en promedio, independientemente de que la diferencia de potencial sea negativa o positiva para el equipo local.

Recalcamos que el procedimiento implementado para la detección de clusters no proporciona una solución incontestable, ya que está sujeto a diferentes discusiones, como cuál es el mejor índice para utilizar en la determinación de clusters (ver Andrews y Currim, 2003), entre los numerosos disponibles: BIC, AIC, AIC3, etc. Ya se comentó al inicio que ningún procedimiento de agregación de casos es completamente objetivo. Sin embargo, no cabe duda de las numerosas investigaciones (ej. Bacher, Wenzig y Vogler, 2004; Magidson y Vermunt, 2002; Vermunt y Magidson, 2005) que apoyan la superioridad de los modelos de clases latentes sobre el algoritmo K-means para determinar el número óptimo de clusters, por lo que creemos que su utilización es un valor añadido de esta investigación. Además, la doble replicación otorga mayor confiabilidad a los resultados.

Está claro que, tal y como apuntaba Winston (2009), la eficiencia en el lanzamiento es el factor de rendimiento más asociado a la victoria. Por tanto, en general, los equipos que sean más eficientes tendrán una mayor probabilidad de victoria a priori en un partido. Pero como también comentamos al principio, los factores de rendimiento no son completamente exógenos, y aunque los equipos deben trabajar para ser más eficaces en el tiro, perder menos balones e ir al rebote ofensivo, éstas no son variables que un equipo pueda modificar fácilmente antes de un partido (es decir, de un partido a otro), ya que son un reflejo de su potencial general, aunque se pueden trabajar tácticamente durante toda la temporada. Esto nos lleva a la discusión sobre la idoneidad de buscar variables exógenas manipulables en baloncesto, que los técnicos puedan utilizar para incrementar la probabilidad de victoria en partidos concretos. Las variables exógenas utilizadas en esta investigación desafortunadamente no son manipulables. Por ello, futuras investigaciones deberían ahondar en este atractivo campo de estudio, que proporcionaría novedosas aportaciones a la investigación en este deporte. Desde aquí, planteamos diversas posibilidades, como la hora en la que se ponen los partidos (parcialmente controlada por los equipos y la liga), las rutinas de concentración antes de los partidos, el tipo de entrenamiento y el tipo de trabajo psicológico realizado por el equipo antes de cada partido, etc. Es obvio que estas variables son mucho más complejas de medir, pero son las que reúnen las características más deseables desde el punto de vista de la intervención, que como hemos apuntado, es la clave para poder realizar inferencias causales de manera plena.

REFERENCIAS BIBLIOGRÁFICAS

Andrews, R. L., y Currim, I. S. (2003). A Comparison of segment retention criteria for finite mixture logit models. Journal of Marketing Research, 40, 235-243.

Arkes, J. (2011). Is controlling the rushing or passing game the key to NFL victories? The Sports Journal, 14.

Bacher J, Wenzig K,, y Vogler M. (2004). SPSS TwoStep Cluster – First Evaluation. Arbeits- und Diskussionspapiere 2004-2, 2.korr. Aufl . Erlangen-Nürnberg: Friedrich-Alexander Universität.

Berri, D. J. (2008). A simple measure of worker productivity in the National Basketball Association. in The Business of Sport, eds. Brad Humphreys and Dennis Howard, editors, 3 volumes, Westport, Conn

Gómez, M. A., Lorenzo, A. y Sampaio, J. (2009). Análisis del rendimiento en baloncesto. ¿Es posible predecir los resultados? Sevilla: Wancelulen

Kline, R. B. (2010). Principles and practice of structural equation modeling ( 3rd ed.). New York: Guilford Press

Magidson, J. y Vermunt. J. K. (2002). Latent Class Models for Clustering: a Comparison with K-means. Canadian Journal of Marketing Research, 20, 36-43.

Martínez, J. A. (2012). Entrenador nuevo, ¿victoria segura? Evidencia en baloncesto / Chaning a coach, guarantee the win? Revista Internacional de Medicina y Ciencias de la Actividad Física y el Deporte, 12 (48), 663-679

Martínez, J.A. (2011b). El uso del porcentaje de victorias en modelos predictivos en la NBA. Revista Internacional de Derecho y Gestión del Deporte, 13.

Pearl, J. (2000). Causality, models and inference. Cambridge, MA: MIT Press

Vermunt, J., y Magidson, J. (2005). Latent GOLD 4.0 User’s Guide. Belmont: Massachusetts, Statistical Innovations Inc.

Wilcox, R. R. (2010). Fundamentals of modern statistical methods. Second Edition. New York: Springer.

Winston, W. L. (2009). Mathletics. New Jersey: Princeton University Press

Wooldridge, J. M. (2003). Introducción a la econometría: Un enfoque moderno. Thomson, Segunda Edición

Xu, R. y Wunsch II, D. C (2009). Clustering. New Jersey: Wiley.

Referencias totales / Total references: 15 (100%) 

Referencias propias de la revista / Journal’s own references: 1 (6,66%)

Download English PDF

Download Spanish PDF